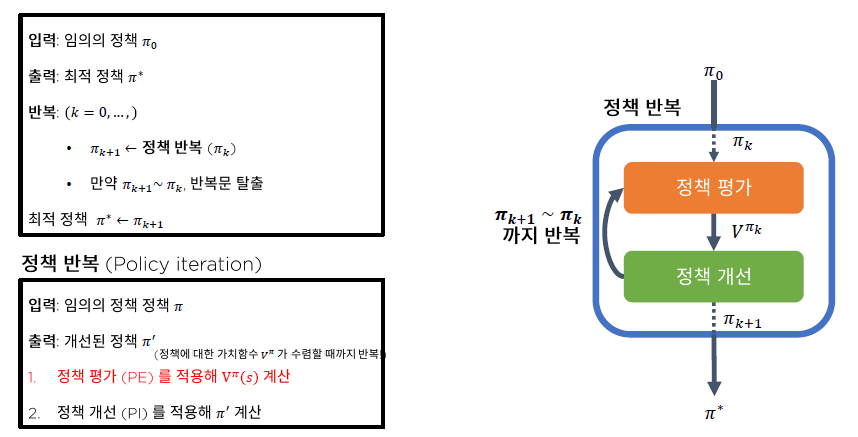
지난 포스트에서 정책반복(정책평가, 정책개선)에 대해 다뤘다.
하지만 몇가지 의문이 생길 수 있다.
그런데 굳이 정책 평가가 수렴할 때 까지 반복해야 할까?
수렴할 때 까지 반복한다면 계산시간의 손해는 없을까?
그렇다면 우선 가치반복이라는 개념에 대해 알아보자.
1) 가치반복(Value Iteration : VI)

가치반복 알고리즘은 정책반복과 다르게 임의의 가치함수 $V_{0}(s)$를 입력으로 주고, 최적 가치함수 $V^{*}(s)$를 받는다.
그림1.의 정책반복 알고리즘과 비교해보면 확연한 차이가 보일 것이다.
정책반복 알고리즘은 최적 정책을 찾기 위해 [(1) $V^{\pi}(s)$도출 -> (2) $Q^{\pi}(s,a)$계산 -> (3) $\pi'$ 계산 -> (4) $\pi'$과 $\pi$의 비교] 이 4단계의 루프를 $V^{\pi}$가 수렴할 때 까지 반복해야한다.
하지만 가치반복 알고리즘의 경우 [최적 가치함수 $V^{*}(s)$의 계산(수렴 까지 반복) -> $Q^{*}(s,a)$계산 -> $\pi^{*}$계산] 이 3단계만 수행하면 최적정책을 찾아낼 수 있다.
한 눈에 봐도 가치반복 알고리즘이 계산이 더 간단해보이고, 빨라 보인다.
하지만, 이번에는 가치반복 알고리즘이 과연 하나의 유일한 값으로 수렴하는지가 관건이다.
여기서도 Bellman optimality backup 오퍼레이터가 등장하는데
$$T^{*}(V) \overset{def}{=} \underset{a \in \cal{A}}{max}(R^{a} + \gamma P^{a}V)$$
의 형태가 된다.
$T^{*}(V)$는 $\gamma$ - 수축 사상이며, $\parallel T^{*}(u) - T^{*}(v) \parallel_{\infty} \leq \gamma \parallel u - v \parallel_{\infty}$을 만족한다.
"바나흐 고정점 정리"에 의해 가치반복 VI는 유일한 해 $V^{*}$로 수렴한다.
가치반복 알고리즘을 Python 코드로 구현하면 다음과 같다.
def value_iteration(self, v_init=None, compute_pi=False):
"""
:param v_init: (np.array) initial value 'guesstimation' (optional)
:param compute_pi: (bool) compute policy during VI
:return: v_opt: the optimal value function
"""
if v_init is not None:
v_old = v_init
else:
v_old = np.zeros(self.ns)
info = dict()
info['v'] = list()
info['pi'] = list()
info['converge'] = None
steps = 0
converged = False
while True:
# Bellman optimality backup
v_improved = (self.R.T + self.P.dot(v_old)).max(axis=0) # [num. actions x num states]
info['v'].append(v_improved)
if compute_pi:
# compute policy from v
# 1) Compute v -> q
q_pi = (self.R.T + self.P.dot(v_improved)) # [num. actions x num states]
# 2) Construct greedy policy
pi = np.zeros_like(self.policy)
pi[np.arange(q_pi.shape[1]), q_pi.argmax(axis=0)] = 1
info['pi'].append(pi)
steps += 1
# check convergence
value_gap = np.linalg.norm(v_improved - v_old)
if value_gap <= self.error_tol:
if not converged: # record the first moment of within error tolerance.
info['converge'] = steps
break
else:
v_old = v_improved
return info전체적인 흐름은 정책반복과 비슷하다.
정책반복과 차이점을 비교하고 싶다면 전 포스트를 참고하면 되겠다.
2) 비동기적 DP 알고리즘 (Asynchronous DP)
여러가지 비동기적 DP 알고리즘이 존재하지만, 이 강의에서는 세가지 알고리즘을 설명한다.
1. In-place DP
2. Prioritized sweeping
3. Real-time DP
세 알고리즘은 PE(Policy Evaluation)/VI(Value Iteration)의 수렴성을 해치지 않는 것으로 증명됨.
먼저, 기존의 동기적 DP알고리즘의 가치 Table 업데이트 형태를 살펴보자.
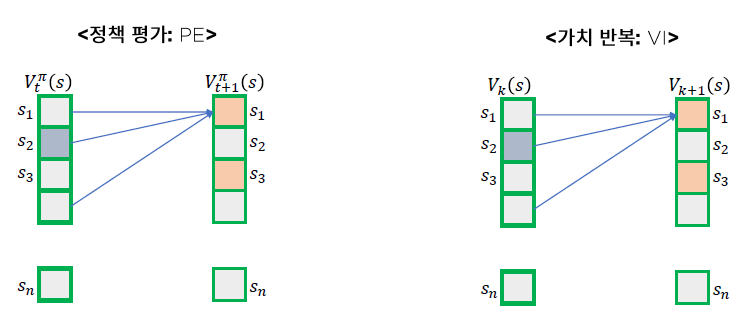
모든 가치 Table이 동시에 업데이트 되는 것을 볼 수 있다.
만약 전체 행동의 경우의 수 (s의 개수)가 커진다면, 계산하기 어려워진다.
행동의 경우의 수가 커진다면, 이 때 비동기적 업데이트 알고리즘이 필요하다.
이전 챕터에서 배웠던 정책평가, 가치반복은 모두 매 반복마다 모든 $(s)$ 및 $(s,a)$에 대해 업데이트 해줬는데, 이 방식들을 Full Sweeping이라고 부른다.
우선, Full Sweeping으로 상태 가치함수를 업데이트한다고 가정하고, 비동기적 DP알고리즘을 구현해보자.
2-1) In-place DP

In-place 연산의 경우 현재 알고있는 가장 새로운 값 $V(s)$를 활용해 $V(s)$들을 업데이트 한다.
장점 :
- 메모리 사용량 절감
- 일반적으로 수렴속도가 더 빠름
- 구현하기 쉬움

In - place 가치반복 알고리즘과 기존 가치반복 알고리즘의 큰 차이는
- value iteration : $V_{k}(s)$와 $V_{k+1}(s)$를 유지하고, $V_{k+1}(s)$를 계산할 때 $V_{k}(s)$를 참조한다.
- In - place value iteration : $V(s)$만을 유지하고, $V(s')$을 계산할 때 $V(s)$를 참조한다.
Full Sweeping 방식의 In-place value iteration을 Python으로 구현하면 다음과 같다.
def in_place_vi(self, v_init=None):
"""
:param v_init: (np.array) initial value 'guesstimation' (optional)
:return:
"""
if v_init is not None:
value = v_init
else:
value = np.zeros(self.ns)
info = dict()
info['v'] = list()
info['pi'] = list()
info['converge'] = None
info['gap'] = list()
steps = 0
# loop over value iteration:
# perform the loop until the value estimates are converge
while True:
# loop over states:
# we perform 'sweeping' over states in "any arbitrary" order.
# without-loss-of-generality, we can perform as the order of states.
# in this example, we consider the "full sweeping" of values.
# perform in-place VI
delta_v = 0
info['v'].append(value)
pi = self.construct_policy_from_v(value)
info['pi'].append(pi)
for s in range(self.ns):
# Bellman expectation backup of current state in in-place fashion
# get Q values of given state 's'
# output of 'self.compute_q_from_v(value)' is a tensor
# with the shape of [num. actions X num. states].
qs = self.compute_q_from_v(value)[:, s]
v = qs.max(axis=0) # get max value along the actions
# accumulate the deviation from the current state s
# the deviation = |v_new - v|
delta_v += np.linalg.norm(value[s] - v)
value[s] = v
info['gap'].append(delta_v)
if delta_v < self.error_tol:
info['converge'] = steps
break
else:
steps += 1
return info※ 이 함수는 Full Sweeping방식을 가정하고 작성하였기 때문에 while문 내 for문이 중첩되어 있고,
기존의 가치반복 알고리즘과 시간적인 부분에서는 큰 차이가 나지 않을 것이며 이 방식은 비현실 적일 것이다.
하지만 추후에 진행하는 방식에는 Partial Sweeping을 사용 할 것이므로 시간적인 이득이 클 것으로 생각한다.
2-2) Prioritized sweeping
Bellman error의 크기가 가장 큰 $s$부터 업데이트 한다.
Bellman error(s) = $|\underset{a \in \cal{A}}{max}(R^{a}_{s} + \gamma \sum_{s' \in S} P_{ss'}^{a} V(s')) - V(s)|$
장점:
- PE/VI의 수렴속도가 빨라짐.
Prioritized Sweeping은 Bellman에러의 크기에 따라 업데이트 우선순위가 부여된다.
Prioritized Seeping Value Iteratin을 Python코드로 구현하면 다음과 같다.
def prioritized_sweeping_vi(self, v_init=None):
"""
:param v_init: (np.array) initial value 'guesstimation' (optional)
:return:
"""
if v_init is not None:
value = v_init
else:
value = np.zeros(self.ns)
info = dict()
info['v'] = list()
info['pi'] = list()
info['converge'] = None
info['gap'] = list()
steps = 0
while True:
# compute the Bellman errors
# bellman_errors shape : [num.states]
bellman_errors = value - (self.R.T + self.P.dot(value)).max(axis=0)
state_indices = range(self.ns)
# put the (bellman error, state index) into the priority queue
priority_queue = PriorityQueue()
for bellman_error, s_idx in zip(bellman_errors, state_indices):
priority_queue.put((-bellman_error, s_idx))
info['v'].append(value)
pi = self.construct_policy_from_v(value)
info['pi'].append(pi)
delta_v = 0
while not priority_queue.empty():
be, s = priority_queue.get()
qs = self.compute_q_from_v(value)[:, s]
v = qs.max(axis=0) # get max value along the actions
delta_v += np.linalg.norm(value[s] - v)
value[s] = v
info['gap'].append(delta_v)
if delta_v < self.error_tol:
info['converge'] = steps
break
else:
steps += 1
return info
여기서, In - place 알고리즘과 눈에 띄는 차이점은
1. PriorityQueue()를 통해 우선순위 큐를 만들어 주고
2. 그 안에 bellman_errors와 state_indices를 넣어주고
3. bellman_error와 s_idx를 꺼내온다는 것이다.
그리고 특이하게 보이는 점은 우선순위 큐에 주는 우선순위에 -bellman_error($-e(s)$)를 준다는 것이다.
우선순위 큐는 우선순위가 낮은 순서 (ex. 1, 2, 3, 4, ...)로 리턴을 해준다.
우리는 Bellman error가 큰 순서 부터 가치함수를 업데이트 해주고 싶기 때문에
우선순위로 들어가는 bellman_error에 (-)를 곱해주는 것이다.
※ 이 함수 또한 Full Sweeping을 가정하였기 때문에 비현실적이고, 업데이트 시간도 크게 차이가 나지 않는다.
2-3) Real-time DP
강화학습의 에이전트가 현재 겪은 상황만 업데이트 한다.
현재상태가 $S_t$라면
$$V(S_t) = \underset{a \in \cal{A}}{max}(R^{a}_{S_t} + \gamma \sum_{s' \in S} P_{S_ts'}^{a} V(s'))$$
3) 동적계획법 한눈에 보기

4) Partial Sweeping Value Iteration
In - place Value Iteration과 Prioritized Sweeping의 코드를 설명하면서 Full Sweeping을 가정했다는 언급을 계속 하며 비현실적이라고도 계속 언급을 했다.
이는 Value Iteration이 수렴함을 보여주기 위해 해당 가정을 놓고 코드를 구현해서 그렇다.
그렇다면 Full Sweeping이 아니더라도 수렴할까?
라는 생각에 대한 답은 "특정 조건이 맞춰지면 그렇다"이다.
여기서 특정조건이란 "모든 가치반복 업데이트 동안 모든 s가 업데이트 될 때"이다.
In - place VI를 Partial Sweeping 방식으로 업데이트 한 예를 살펴보자.
def in_place_vi_partial_update(self,
v_init=None,
update_prob=0.5,
vi_iters: int = 100):
"""
:param v_init: (np.array) initial value 'guesstimation' (optional)
:return:
"""
if v_init is not None:
value = v_init
else:
value = np.zeros(self.ns)
info = dict()
info['v'] = list()
info['pi'] = list()
info['gap'] = list()
# loop over value iteration:
# perform the loop until the value estimates are converge
for steps in range(vi_iters):
# loop over states:
# we perform 'sweeping' over states in "any arbitrary" order.
# without-loss-of-generality, we can perform as the order of states.
# in this example, we consider the "full sweeping" of values.
# perform in-place VI
delta_v = 0
for s in range(self.ns):
perform_update = np.random.binomial(size=1, n=1, p=update_prob)
if not perform_update:
continue
# Bellman expectation backup of current state in in-place fashion
# get Q values of given state 's'
qs = self.compute_q_from_v(value)[:, s]
v = qs.max(axis=0) # get max value along the actions
# accumulate the deviation from the current state s
# the deviation = |v_new - v|
delta_v += np.linalg.norm(value[s] - v)
value[s] = v
info['gap'].append(delta_v)
info['v'].append(value.copy())
pi = self.construct_policy_from_v(value)
info['pi'].append(pi)
return info
2-1)에서 본 In - place DP와 차이점이 보이는가?
차이점을 살펴보자면 크게 두가지가 있다.
1. 함수의 인수에 update_prob가 추가되었다.
update_prob인수는 for s in range(self.ns) 밑
perform_update = np.random.binomial(size=1, n=1, p=update_prob)
구문에서 사용 되는데, perform_update는 1 또는 0로 반환된다.
업데이트는 상태 1, 2, 3, ..., ns를 돌면서 수행하는데, 만약 특정 s에서 perform_update가 0이라면 그 상태에 대한 업데이트는 진행하지 않고, 1이라면 그 상태에 대해 업데이트를 진행한다.
2. 또한, 인수에 vi_iters가 추가되었다. 즉 몇번의 가치반복을 수행할 것인지 추가한 것이다.
이 함수를 통해 가치반복을 수행하면 vi_iters가 충분히 큰 경우 가치함수가 수렴하는 것을 확인 할 수 있다.
따라서, 충분한 iteration이 존재하는 경우에는 Partial Sweeping이더라도
우리가 원하는 최적가치 함수로 수렴할 것이라는 것을 알 수 있다.
내 생각 :
Partial Sweeping과 Full Sweeping의 차이에 대해 알 수 있었고, 현업에 적용하기에 둘은 상당한 차이가 있을 것으로 생각하게 되었다.
보통은 강화학습에 사용되는 데이터의 크기가 방대할 것으로 생각하기 때문에 Partial Sweeping은 필수이되 iteration의 수가 적절히 잘 조정되어야 할 것같다.
정책반복과 가치반복의 차이, 동기적 DP와 비동기적 DP의 차이를 효율성을 따져 기억한다면 실전에서 사용할 때 효율적인 코딩이 될 것 같다.
참고자료 :
강화학습 A-Z 강의자료
'강화학습 강의 복습노트' 카테고리의 다른 글
| Part2 - 6. Temporal Difference(TD) 정책추정 (0) | 2020.12.25 |
|---|---|
| Part2 - 5. 몬테 카를로 정책추정 (Monte-carlo prediction: MC prediction) (0) | 2020.12.25 |
| Part2 - 3. 동적계획법 (Dynamic Programming) (0) | 2020.12.23 |
| Part2 - 2. MDP(Markov Decision Processes) (0) | 2020.12.21 |
| Part2 - 1. MP, MRP (0) | 2020.12.21 |



