지난 포스트까지는 환경에 대한 정보가 주어질 때를 가정하였을 때의 강화학습 풀이기법인 동적계획법 (Dynamic Processing : DP)를 살펴보았다.

정책 반복에서 가치반복으로, 가치반복에서 비동기 DP기법으로 점점 더 효율적인 알고리즘을 찾기 위해 배웠던 것들이 생각난다.
이 방법은 매우 효율적이긴 하지만, 실제 현업에서는 보상 $R^{\pi}$, 상태 천이 매트릭스 $P^{\pi}$ 등 환경에 대한 정보를 미리 안다는 것 자체가 거의 불가능하다.
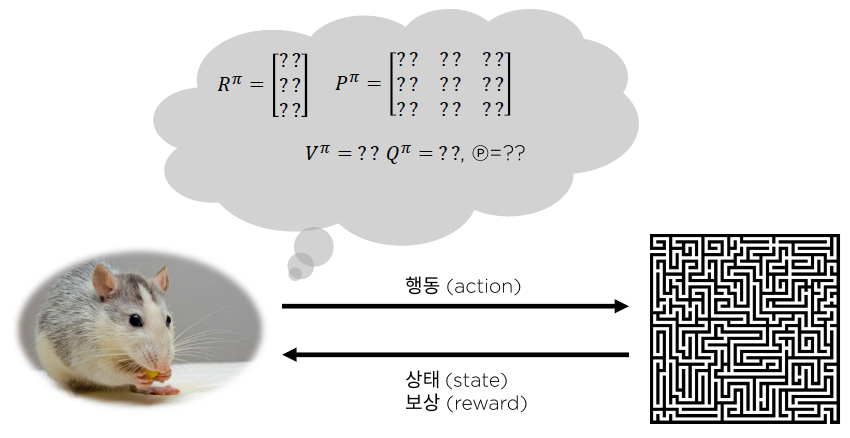
따라서, 환경에 대한 지식이 없기 때문에
환경과 상호작용을 통해 가치함수 및 정책 혹은 환경의 모델을 추산한다.
강화학습 템플릿을 살펴보면
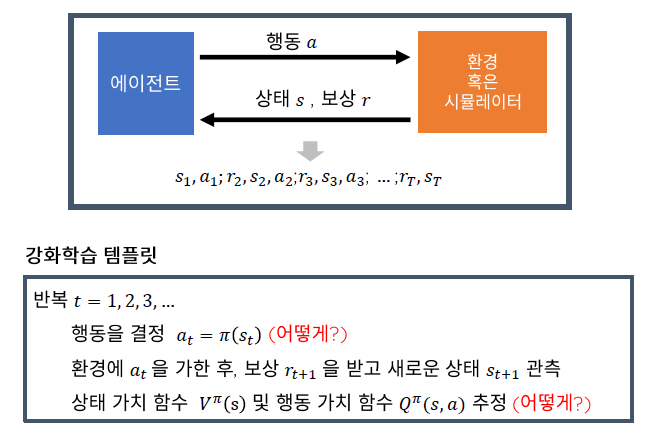
행동을 결정하기 위해서는 정책 함수 $\pi(s_t)$가 필요하고, $\pi(s_t)$를 구하기 위해서는 상태가치함수 $V^{\pi}(s)$를 이용해 추정한 행동 가치함수 $Q^{\pi}(s,a)$가 필요하다. 하지만 $\pi(s_t)$와 $V^{\pi}(s)$를 어떻게 구할까?
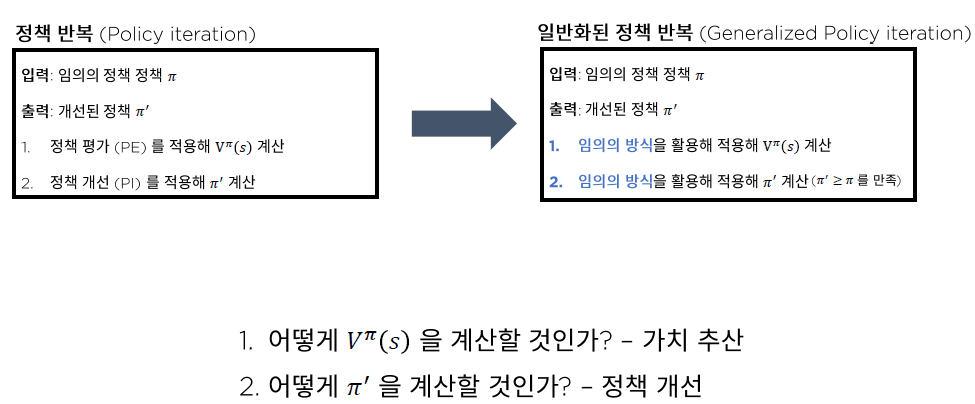
이전 포스트까지 다루었던 정책반복은 일반화된 정책반복의 일부분이다.(포함관계)
일반화된 정책반복을 보면 임의의 방식을 활용해 $V^{\pi}(s)$를 구하고, $\pi'$을 구하는 것을 볼 수 있다.
$\pi'$을 구할 때 정책 개선을 사용하고, $V^{\pi}(s)$를 구할 때 가치 추산을 사용한다고 하는데
가치 추산을 위해 사용하는 알고리즘은 여러가지가 존재한다.
1) Model free 가치 추산 알고리즘의 분류
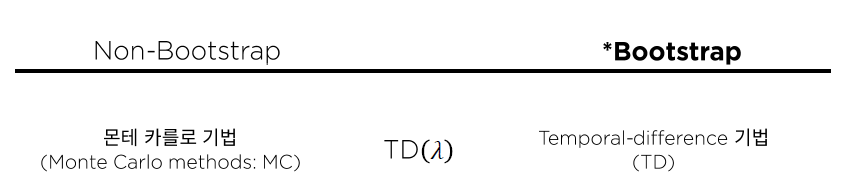
가치 추산 알고리즘은 Non-Bootstrap기법인 (1) 몬테 카를로 기법과 Bootstrap기법인 (2) Temporal-difference기법으로 나눌 수 있다.
통계학에서 Bootstrap이란 모수의 분포를 추정하기 위해 현재의 표본에서 추가적으로 표본을 추출한 뒤 각 표본에 대한 통계량을 다시 계산하는 것이다. 이는 샘플이 부족한 경우나 더 정확한 신뢰구간을 구하기 위해 주로 사용하는데, 자세한 사항은 링크를 참조하면 될 것같다.
DATA - 12. 부트스트랩(Bootstrap)
부트스트랩(Bootstrap) 모수의 분포를 추정하는 파워풀한 방법은 현재 있는 표본에서 추가적으로 표본을 복원 추출하고 각 표본에 대한 통계량을 다시 계산하는 것입니다. 이러한 절차를 부트스트
bkshin.tistory.com
2) 몬테 카를로 기법
정의 :
계산하기 어려운 값을 수 많은 확률 시행을 거쳐 추산하는 기법.
(즉, 여러번의 시뮬레이션을 통해 값을 산출하는 기법이라고 보면 된다.)
예 :
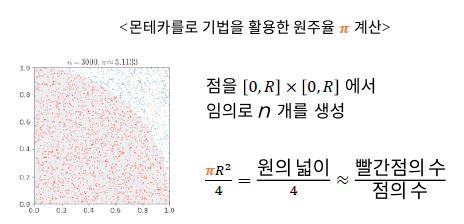
그림6.의 예는 원주율 $\pi$를 계산하는 예이다.
좌표평면은 1 * 1 평면이고 원의 1/4에 해당하는 부분을 경계로 두어 빨간점은 경계 안쪽, 파란점은 경계 바깥쪽에 찍도록 했을 때, 무수히 많은 점을 찍고 빨간점의수 / 모든점의 수를 계산한다면 원의 넓이($\pi R^2$)/4와 비슷할 것이다. 이를 이용해 $\pi$를 계산할 수 있는 것이다.
이와 같이 확률적인 방법을 통해 어떤 값을 추산하는 방법을 몬테 카를로 기법이라고 한다.
자세한 사항은 링크를 참고하도록 하자.
몬테카를로 방법과 인공지능 – Sciencetimes
www.sciencetimes.co.kr
3) 몬테 카를로 기법을 활용한 가치 함수 추산
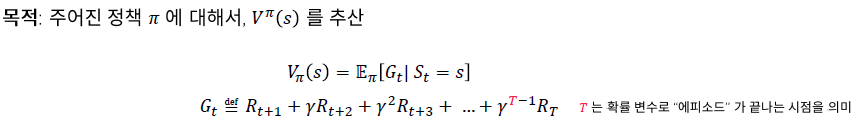
기존의 $V^{\pi}(s)$를 구하는 방법은 그림7.과 같다.
하지만 우리는 환경에 대한 정보가 없다. (즉, $R_t$에 대한 정보가 없다.)
그래서 몬테 카를로 기법에서는 여러번의 시뮬레이션을 통해 $R_t$ 및 $G_t$에 대한 정보를 얻는 과정이 필요하다.
몬테 카를로 기법으로 $V^{\pi}(s)$를 구하는 방법은 다음과 같다.

여러번의 시뮬레이션 후 $G_t$의 평균을 계산하면 $V^{\pi}(s)$와 비슷해진다. (불편 추정치)
즉,
$$V(s) = \frac{G(s)}{N(s)}$$
($G(s)$는 리턴 추산치의 합, $N(s)$는 상태 s의 방문 횟수)
4) 몬테 카를로 정책 추정
몬테 카를로 정책추정의 방식은 두가지가 있다.
(1) 최초 방문 몬테 카를로 정책 추정
- 에피소드내에서 최초로 방문한 s에 대해서만 리턴을 계산
(2) 모든 방문 몬테 카를로 정책 추정
- 에피소드내에서 방문한 모든 s에 대해서 리턴을 계산
4-1) 최초 방문 몬테 카를로 정책 추정

그림9.와 같이
3가지의 상태($s^{1}, s^{2}, s^{3}$)와
3가지의 행동($a^{1}, a^{2}, a^{3}$)을 가지며
3개의 에피소드(반복)을 Terminal상태(종결상태)까지 수행한다고 가정해보자.
에피소드 내에서 각 단계는 ($s_t$ : t번째 방문, $a_t$ : t번째 수행한 행동, $r_t$ : t번째 획득한 보상)으로 이루어져 있다.
이때 에피소드 내에서 최초로 방문한 $s^{1}$에 대해서만 리턴을 계산한다고 했을 때,

(감가율 $\gamma$는 1로 가정)
그림10.과 같이 3개의 $G_t$가 나오며, 3개의 $G_t$에 대한 산술평균을 계산하여 $V^{\pi}(s^1)$을 구한다.
4-2) 모든 방문 몬테 카를로 정책 추정

최초 방문 몬테 카를로 가치 추정의 예와 동일한 환경이 주어져있다고 가정해보자.
그렇다면 방문한 모든 $s^{1}$에 대해 리턴을 계산하면 어떻게 될까?

(감가율$\gamma$는 1로 가정)
그림12.와 같이 6개의 $G_t$가 나오며, 6개의 $G_t$에 대한 산술 평균을 계산하여 $V^{\pi}(s^1)$을 구한다.
그렇다면 최초 방문 MC vs 모든 방문 MC 둘중 무슨 방식을 써야하는가?
- 현실에서는 모든 방문 MC가 선호되는 편이라고 한다.
위에서 계산한 예는 추가적인 데이터가 발생하지 않을 때를 가정하고 계산하기 때문에 배치(batch)산술평균 방식이라 할 수 있다.
그렇다면 추가적인 데이터가 지속적으로 발생하는 경우라면 위와같이 배치방식으로 계산하는 것이 옳을까?
대답은 No!일 것이다.
추가적인 데이터가 발생하는 경우 기존의 모든 $G_t$를 저장해야하고, 메모리 효율이 매우 떨어지기 때문이다.
그래서 추가적인 데이터에 대해서만 계산을 한 후, 업데이트 하는 방식이 필요해보인다.
이를 온라인 평균기법이라한다.
5) 배치 산술평균을 온라인 평균기법으로 변환

그림13.에 따르면 k번째 데이터가 추가적으로 관측 된다고 했을 때,
k-1번째 데이터까지의 평균 + $\frac{1}{k}$[ k번째 관측 값 - (k-1)번째 데이터까지의 평균 ]이
k번째 데이터까지의 평균이 됨을 볼 수 있다.
6) Incremental MC policy evaluation
온라인 기법을 MC기법에 적용하면 Incremental MC기법이라고 부른다.

Incremental MC기법을 적용하면 추가적으로 발생하는 데이터에 대해 효율적인 계산이 가능하나
현실에서는 $N(s)$를 세는 것 조차 어려운 경우가 있다.
따라서 $N(s)$ 대신 학습률(learning rate : $\alpha$)을 적용할 수 있다.
이 논문을 보면 적당히 작은 $\alpha$에 대해 참값으로 수렴함이 증명되어있다.
지금까지 상태 가치함수 $V^{\pi}(s)$를 MC기법으로 구하는 방법에 대해 알아보았다.
하지만 정책개선 수행을 위해서는 $Q^{\pi}(s,a)$가 필요하다.
7) MC를 활용한 행동 가치함수 추산
행동 가치 함수 추산의 경우 상태 s 뿐만 아니라 행동 a에 대해서도 고려해주어야 한다.
전체적인 계산 매커니즘은 위에서 본 MC 정책 추정과 비슷하다.
또 한번 예를 보겠다.

이번 예에서는 최초로 방문한 ($s^1, a^2$) 쌍(pair)에 대해서 리턴을 계산하는 것이 목적이다.
($Q^{\pi}(s^1, a^2)$를 구하기 위함)
이를 계산한다면

(감가율 $\gamma$는 1로 가정)
위에서 본 $V^{\pi}(s, a)$계산 방식과 유사하게 $Q^{\pi}(s,a)$를 구하는 것을 볼 수 있다.
행동 가치함수 추산 역시
(1) 방문한 모든 행동가치함수 추산이 가능하며
(2) Incremental한 방식의 추산도 가능하다.
상태 가치함수와 행동 가치함수를 MC기법으로 구하는 함수를 Python코드로 구현하면 다음과 같다.
total_eps = 2000
log_every = 500
def run_episodes(env, agent, total_eps, log_every):
mc_values = []
log_iters = []
agent.reset_statistics()
for i in range(total_eps+1):
run_episode(env, agent)
if i % log_every == 0:
agent.compute_values()
mc_values.append(agent.v.copy())
log_iters.append(i)
info = dict()
info['values'] = mc_values
info['iters'] = log_iters
return info
- 알고리즘 내 변수 및 함수 설명 -
함수명이 run_episodes인 이유는 MC기법은 한 에피소드를 돌고 난 후, 업데이트를 진행하므로 여러 에피소드를 돌린다는 의미에서 run_episodes이다
함수가 워낙 많고 변수도 워낙 많아서 헷갈릴 수 있을 것 같아 중요한 요소들에 대해서만 정리하도록 하겠다.
추후에 코드 정리를 한번 해서 올릴 예정이다..
run_episode(env, agent) :
def run_episode(env, agent):
env.reset()
states = []
actions = []
rewards = []
while True:
state = env.observe()
action = agent.get_action(state)
next_state, reward, done, info = env.step(action)
states.append(state)
actions.append(action)
rewards.append(reward)
if done:
break
episode = (states, actions, rewards)
agent.update(episode)- 인수로 환경과 에이전트를 받는다.
- env. observe()함수로 현재 상태를 받는다.
- get_action(state)로 현재 상태를 입력해 다음 행동을 받는다.
- env.step(action)으로 행동을 부여해 다음 상태, 보상, 종결여부, info를 받는다.
- 모든 state와 action과 reward를 기록한다.
- 이 반복은 종결상태가 될 때까지 반복한다.
- 종결상태에 이르면 agent.update(episode)함수로 agent를 업데이트 해준다.
vanilla version의 agent.update(episode) :
def update(self, episode):
states, actions, rewards = episode
# reversing the inputs!
# for efficient computation of returns
states = reversed(states)
actions = reversed(actions)
rewards = reversed(rewards)
iter = zip(states, actions, rewards)
cum_r = 0
for s, a, r in iter:
cum_r *= self.gamma
cum_r += r
self.n_v[s] += 1
self.n_q[s, a] += 1
self.s_v[s] += cum_r
self.s_q[s, a] += cum_r- episode를 인수로 받는다.
- states(상태), actions(행동), rewards(보상) 리스트들을 뒤집어준다.
※ 여기서, 뒤집어 주는 이유를 설명하자면

만약 위의 그림에서 $s^{1}$에 대해 모든 리턴을 계산하고자 한다면 빨간색 화살표에 해당하는 계산(총 6회)을 해야한다.
하지만 파란색의 그림처럼 역순으로 계산해주면서 $s^{1}$에 대해서만 기록한다면 파란색 화살표에 해당하는총 3회에 해당하는 계산만 하며 기록해주면 된다.
"한마디로 그냥 계산을 효율적으로 하기 위한 처리이다."
- 리스트를 역행하며 s상태에 도달한 횟수, s상태의 감가된 보상의 합 등을 self.n_v, self.s_v등에 기록해준다.
- 이후에는 다시 run_episode로 돌아가고, run_episode함수도 종결되므로 run_episodes로 빠져나간다.
Incremental version의 agent.update(episode) :
def update(self, episode):
states, actions, rewards = episode
# reversing the inputs!
# for efficient computation of returns
states = reversed(states)
actions = reversed(actions)
rewards = reversed(rewards)
iter = zip(states, actions, rewards)
cum_r = 0
for s, a, r in iter:
cum_r *= self.gamma
cum_r += r
self.v[s] += self.lr * (cum_r - self.v[s])
self.q[s, a] += self.lr * (cum_r - self.q[s, a])- episode를 인자로 받는다.
- vanilla version의 update함수와 비슷하나 차이점은 $N(s)$를 계산하지 않으며, learning rate(lr)을 사용하는 것이다.
- Incremental version의 update함수의 계산식은 다음과 같다.
$$V(s) \leftarrow V(s) + \alpha (G_t - V(s))$$
agent.compute_values() :
리턴의 추산치와 각 상태 s 및 상태,행동(s, a)의 방문횟수를 활용하여 상태가치함수 $V$와 행동가치함수 $Q$를 계산
def compute_values(self):
self.v = self.s_v / (self.n_v + self._eps)
self.q = self.s_q / (self.n_q + self._eps)- log_every번째마다 가치함수를 기록할 때, 호출되는 함수
- MC 기법의 상태가치함수와 행동가치함수의 계산
$$ V(s) \leftarrow \frac{G(s)}{N(s)} $$
$$ Q(s,a) \leftarrow \frac{G(s, a)}{N(s, a)}$$
- self._eps의 역할 : 만약 self.n_v나 self.n_q가 0이어서 0으로 나누어지는 것을 방지하기 위함
8) MC기법의 장,단점
(1) 장점 :
- 환경에 대한 선험적 지식이 필요 없음
- 직관적이고 구현하기 쉬움
- 항상 정확한 가치 함수 값을 계산함
(2) 단점 :
- Episode가 끝나야만 적용이 가능
- DP와는 다르게 각 상태와 행동의 관계에 대해서 전혀 활용하지 않음
- 정확한 값을 얻기 위해 많은 시뮬레이션을 필요로 함 (일반적으로 수렴 속도가 느림)
내 생각:
코드가 여러가지 섞이면서 더더욱 알아볼수가 없게 만들어진 것 같다.
코드를 동반 할 때 최대한 이해하기 쉽도록 설명하고 싶었으나. 그게 불가능할 것 같다.
추후에 코드 정리를 한 포스팅도 따로 해야할 것 같다.
MC에 대해 복습을 하고나니 나에게는 장점보다는 단점이 더 부각되어 보이는 것 같다.
현실 적용 시 episode가 끝나지 않는 경우도 있을 것이고, 수많은 시뮬레이션을 필요로 하는 것도 큰 disadvantage로 느껴진다.
참고자료 :
부트스트랩 : bkshin.tistory.com/entry/DATA-12
학습률의 참값 수렴 증명 : projecteuclid.org/download/pdf_1/euclid.aoms/1177729586
강화학습 A-Z 강의자료
'강화학습 강의 복습노트' 카테고리의 다른 글
| Part2 - 7. MC Control : MC기법을 활용한 최적 정책 찾기 (0) | 2020.12.26 |
|---|---|
| Part2 - 6. Temporal Difference(TD) 정책추정 (0) | 2020.12.25 |
| Part2 - 4. 비동기적 동적계획법 (0) | 2020.12.23 |
| Part2 - 3. 동적계획법 (Dynamic Programming) (0) | 2020.12.23 |
| Part2 - 2. MDP(Markov Decision Processes) (0) | 2020.12.21 |



