1) 동적계획법 (Dynamic Programming : DP)
정의 : 복잡한(큰) 문제를 작은 문제로 나눈 후 -> 작은 문제의 해법을 조합해 큰 문제의 해답을 구하는 기법
동적계획법이 강화학습과 무슨상관인가? 라는 의문이 들 지도 모르겠다.
* 동적계획법으로 해결할 수 있는 문제의 특징
1. 최적 하위구조
- 큰 문제를 분할한 작은 문제의 최적값이 큰 문제에서도 최적값임
2. 중복 하위문제
- 큰 문제의 해를 구하기 위해서, 작은 문제의 최적해를 재사용.
MDP에서 정의한 Bellman 기대/최적 방정식은 위의 두 특성을 모두 만족시킨다.
즉, DP를 활용해 Bellman 기대/최적 방정식의 해를 효율적으로 계산할 수 있다는 것이다.
지난 포스트에서 다룬 Bellman 기대/최적 방정식을 다시 살펴보면


$V_{\pi}(s)$, $Q_{\pi}(s,a)$와 $V^{*}(s)$, $Q^{*}(s,a)$를 각각 재귀형식으로 구하는 수식을 볼 수 있다.
동적계획법을 사용하여 위의 재귀식을 구현한다면 기존보다 더 효율적인 계산이 가능하다.
2) 정책평가(policy Evaluation : PE)
목적 : $V^{\pi}(s)$를 구하는 것

이 알고리즘을 순서대로 해석하면
1. 우선 상태 가치함수 $V_{0}^{\pi}(s)$를 초기화 한다. (이때 꼭 0이 아니어도 된다.)
2. 그리고 앞에서 구한 행렬표현을 활용해 각 상태 s에 대하여 $V_{t+1}^{\pi}(s)$를 구한다.
3. 이 반복을 $\underset{s \in \cal{S}}{max} |V_{t+1}^{\pi}(s) - V_{t}^{\pi}(s)| \leq \epsilon$이 만족할 때까지 반복한다.
여기서 $\epsilon$이 처음 등장하는데, $\epsilon$은 매우 작은 수를 뜻한다.
말 그대로 해석하면, 개선된 상태 가치함수와 기존 상태 가치함수간의 차이가 거의 없을 때
(즉, 어느 값으로 수렴할 때) 해당 반복을 중단하겠다는 뜻이다.
동적 계획법으로 정책평가 알고리즘을 Python코드로 구현하면 다음과 같다.
def policy_evaluation(self, policy=None, v_init=None):
"""
:param policy: policy to evaluate (optional)
:param v_init: initial value 'guesstimation' (optional)
:return: v_pi: value function of the input policy
"""
if policy is None:
policy = self.policy
r_pi = self.get_r_pi(policy) # [num. states x 1]
p_pi = self.get_p_pi(policy) # [num. states x num. states]
if v_init is None:
v_old = np.zeros(self.ns)
else:
v_old = v_init
while True:
# perform Bellman expectation backup
v_new = r_pi + self.gamma * np.matmul(p_pi, v_old)
# check convergence
bellman_error = np.linalg.norm(v_new - v_old)
if bellman_error <= self.error_tol:
break
else:
v_old = v_new
return v_new
- 정책 평가 알고리즘 내 변수 및 함수 설명 -
self : 동적 계획법의 Agent
동적계획법은 원래 Agent의 개념을 사용하지 않지만 강화학습의 구현 템플릿에 대한 이해를 돕기위해 만든 Agent
Agent의 기본 특성들은
class TensorDP:
def __init__(self,
gamma=1.0,
error_tol=1e-5):
...과 같이 설정 되며, gamma는 감소율, error_tol는 수치적 에러의 허용치 그림3. 에서는 $\epsilon$이고
환경을 설정해주는 함수
def set_env(self, env, policy=None):
self.env = env
if policy is None:
self.policy = np.ones([env.nS, env.nA]) / env.nA
self.ns = env.nS
self.na = env.nA
self.P = env.P_tensor # Rank 3 tensor [num. actions x num. states x num. states]
self.R = env.R_tensor # Rank 2 tensor [num. actions x num. states]에서 환경에 대한 정보를 가지는 env인자를 받아 정책(policy), 상태천이함수(P), 보상함수(R)을 초기화한다.
policy : 정책함수 $\pi$
- $\pi$의 형태는 다음과 같다.
- (상태의 수, 행동의 수)로 이루어진 Matrix의 형태이며
- (i행, j열)의 요소는 i번째 상태일 때, j번째 행동을 할 확률이다.

get_r_pi : $R^{\pi}_s$ 계산
- 이전 포스트를 참고하면 $R^{\pi}_s$는
$$R^{\pi}_s = \sum_{a \in \cal{A}} \pi(a|s) R_s^a$$
의 형태를 가지고 있으며
- $\pi$(상태의 수, 행동의 수)와 $R$(상태의 수, 행동의 수)를 이용하여 계산한다.
def get_r_pi(self, policy):
r_pi = (policy * self.R).sum(axis=-1) # [num. states x 1]
return r_pi- 이 코드를 보면 정책함수$\pi$와 보상함수$R$를 요소곱 한 후, 2번째 차원 (즉, 상태의 수 별로) 합을 해준다.
- 이는 $\sum_{a \in \cal{A}}$ 를 구현한 것으로 보면 될 것 같다.
get_p_pi : $P_{ss'}^{\pi}$ 계산
- 이전 포스트를 참고하면 $P_{ss'}^{\pi}$는
$$P^{\pi}_{ss'} = \sum_{a \in \cal{A}} \pi(a|s) P_{ss'}^a$$
의 형태를 가지고 있으며
- $\pi$(상태의 수, 행동의 수)와 $P_{ss'}^{a}$(행동의 수, 상태의 수, 다음 상태의 수)를 이용하여 계산한다.
def get_p_pi(self, policy):
p_pi = np.einsum("na,anm->nm", policy, self.P) # [num. states x num. states]
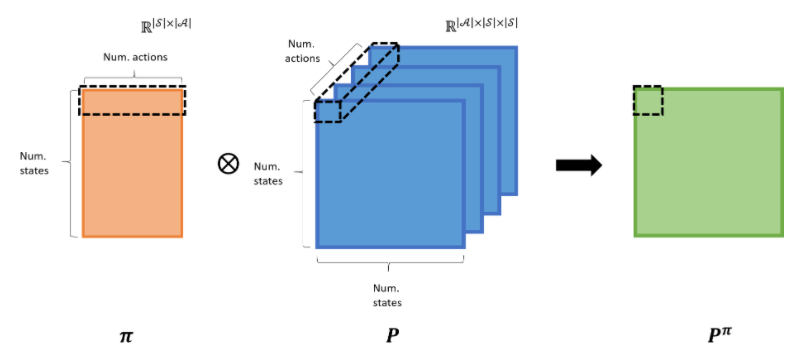
return p_pi- 여기서 '아인슈타인 합(einsum)'이 등장하는데 이는 2차원인 정책함수($\pi$)와 3차원인 상태천이함수($P_{ss'}^{a}$)의 텐서들을 밑 그림에서의 점선과 같은 형태로 계산하기 위함이다.
- 계산 결과, 정책$\pi$를 따르는 $P^{\pi}$(상태의 수, 상태의 수)의 2차원 Matrix가 반환된다.
- np.einsum함수에 대한 자세한 사항은 여기를 참고하기 바란다.
Einsum에 대해 간략한 정리 - 수원혼모노이현성
Einsum Notation Note Pytorch나 Tensorflow 내의 많은 글들이 외우기 너무너무너무 진짜 외우기도 어렵고, 쓰기도 어려워서, 쉽게 표현할 방법이 없나 찾아보다 정리한 글입니다. 기본적으로, Einsum is All You
ita9naiwa.github.io
v_init : $V_{0}^{\pi}(s)$
- 변수는 초기 가치함수의 값을 지정해주는 것이나 모두 0으로 설정하고 싶다면 입력하지 않으면 된다.
3) 정책개선 (Policy Improvement : PI)
목적 : $\pi'$을 구하는 것

이 알고리즘은 정책 평가 알고리즘의 결과로 받은 $V^{\pi}(s)$를 입력하여 개선된 정책 $\pi'$를 출력하는 함수이다.
1. $V^{\pi}(s')$과 $Q^{\pi}(s,a)$의 관계식을 활용해 $Q^{\pi}(s,a)$를 계산 한 후
2. 각 상태에서 $Q^{\pi}(s,a)$가 최고의 값을 가지는 행동의 인덱스를 추출하여 $\pi'(a | s)$의 해당 인덱스에 1을, 나머지에는 0을 넣는다. (이를 greedy improvement라 한다)
3. 개선된 정책 $\pi'(a | s)$ 반환
이 알고리즘을 Python 코드로 구현하면 다음과 같다.
def policy_improvement(self, policy=None, v_pi=None):
if policy is None:
policy = self.policy
if v_pi is None:
v_pi = self.policy_evaluation(policy)
# (1) Compute Q_pi(s,a) from V_pi(s)
r_pi = self.get_r_pi(policy)
q_pi = r_pi + self.gamma * self.P.dot(v_pi)
# (2) Greedy improvement
policy_improved = np.zeros_like(policy)
policy_improved[np.arange(q_pi.shape[1]), q_pi.argmax(axis=0)] = 1
return policy_improved
위 코드에서 q_pi를 행렬 곱의 형태로 구하는 것을 볼 수 있다.
개선된 정책 policy_improved를 입력받은 policy와 같은 형태로 초기화하는데 이때, 모든 요소를 0으로 초기화한다.
그 다음, policy_improved[np.arange(q_pi.shape[1]), q_pi.argmax(axis=0)] = 1를 통해
특정 $s$에 대해 가장 큰 $Q(s,a)$를 만족하는 $a$만을 1.0 으로 설정해준다.
이 알고리즘을 통해 구해진 $\pi'$는 항상 $\pi' \geq \pi$를 만족하게 되는데
이를 정책 개선 정리를 통해 증명 할 수 있다. 자세한 사항은 더보기를 참고하기 바란다.


4) 정책 반복(Policy Iteration) : 정책 평가(PE) + 정책 개선(PI)
정책 반복 알고리즘은 정책 평가와 정책 개선 알고리즘을 하나로 합친 알고리즘이다.
입력으로 임의이 정책 $\pi_0$를 주면 개선된 정책 $\pi'$를 출력으로 뱉는다.

위의 정책반복 알고리즘을 사용하면 MDP에서 Bellman 최적 방정식(Bellman Optimality Equation : BOE) 을 통해 최적 정책을 구했던 것 처럼
DP에서도 최적 정책을 구할 수 있게 된다.

그림 10.에서 보이는 것 같이 $\pi_{k}$가 $\pi_{k+1}$ 와 거의 유사할 때 까지
(즉 정책에 대한 가치함수 $V^{\pi}$가 수렴 할 때 까지)
정책반복을 시행하면 최적정책 $\pi^{*}$를 구할 수 있다.
이 알고리즘을 Python으로 구현하면 다음과 같다.
def policy_iteration(self, policy=None):
if policy is None:
pi_old = self.policy
else:
pi_old = policy
info = dict()
info['v'] = list()
info['pi'] = list()
info['converge'] = None
steps = 0
converged = False
while True:
v_old = self.policy_evaluation(pi_old)
pi_improved = self.policy_improvement(pi_old, v_old)
steps += 1
info['v'].append(v_old)
info['pi'].append(pi_old)
# check convergence
policy_gap = np.linalg.norm(pi_improved - pi_old)
if policy_gap <= self.error_tol:
if not converged: # record the first moment of within error tolerance.
info['converge'] = steps
break
else:
pi_old = pi_improved
return info알고리즘 구동순서
(1) $\pi_0$ 초기화 -> (2) $V^{\pi}_{k}$ 계산 -> (3) $\pi'_{k+1}$ 계산 -> (4) $\pi_{k+1}$와 $\pi_{k}$의 차이 계산 -> (5) 차이가 $\epsilon$보다 작은지 확인 (수렴여부 확인) -> 수렴했다면 while문 빠져나감 or 수렴하지 않았다면 $\pi_{k+1}$를 $\pi_{k}$로 설정해주고 (2)로 돌아감
info는 무엇인가?
info는 가치함수 $V^{\pi}$들을 저장하는 리스트, 정책함수 $\pi_{k}$들을 저장하는 리스트, 최초로 수렴한 스텝 "converge"를 가지는 dictionary
5) MDP와 DP

Bellman 기대값/최적방정식을 활용해 최적 가치함수를 계산 -> 정책 반복 알고리즘을 통해 효율적으로 계산
그런데 아직 정책 평가 알고리즘이 과연 유일한 정답으로 수렴하는가? 에 대한 문제를 해결하지 못했다.
이는 Bellman expectation backup 오퍼레이터, 바나흐 고정점 정리를 통해 해결이 가능하다.
6) Bellman expectation backup 오퍼레이터(연산자)
정의
$$ T^{\pi}(V) \overset{def}{=} R^{\pi} + \gamma P^{\pi}V$$
<$\gamma$ - 수축 사상>
$T^{\pi}(\cdot)$을 일종의 함수라고 고려했을 때, $T^{\pi}(\cdot)$는 '$\gamma$ - 수축 사상'이다.
즉, $T^{\pi}(u)$와 $T^{\pi}(v)$사이의 거리는 $u$와 $v$사이의 거리보다 가깝다.

여기서, $P^{\pi}$의 모든 요소는 0에서 1 사이이므로 증명이 성립한다.
7) 바나흐 고정점 정리
완비 거리공간 $v$에서 정의된 오퍼레이터 $T(v)$가 $\gamma$ - 축약사상이면 다음이 성립한다.
1. $T(v)$를 계속 적용하면 $v$는 유일한 고정점 $v^{*}$로 수렴한다.
2. 이때 수렴속도는 $\gamma$이다.
* 완비 거리공간에 대한 정의는 잘 이해가 되지않아 링크를 첨부했습니다.
8) 정책 평가 알고리즘과 바나흐 고정점 정리
1. 정책 평가 알고리즘의 하나의 반복은 $T^{\pi}(V) \overset{def}{=} R^{\pi} + \gamma P^{\pi}V$이다.
2. $T^{\pi}(\cdot)$은 $\gamma$ - 축약사상이다.
3. $V$들은 완비 거리공간 안에 있다.
4. $V^{\pi}$는 Bellman 기대값 방정식의 유일한 해다.
(1) V가 "완비 거리공간" 조건을 만족, (2) $T^{\pi}(v)$ "$\gamma$ - 축약사상" 조건을 만족하므로
"바나흐 고정점 정리"에 의해 유일해가 존재함을 보일 수 있다. 그때 유일해는 $V^{\pi}$
즉, 임의의 V에 $T^{\pi}(\cdot)$을 연속적으로 적용하면 $V_{\pi}$가 된다.

내 생각 :
코드까지 섞이니 더 어려워보인다.. 바나흐 고정점 정리는 뭔지, 완비거리공간은 뭔지..
기반 지식이 부족해서 증명에 관한 부분이 이해가 잘 가지 않는다.
또한, $P^{\pi}$를 구할 때 $P_{ss'}^{a}$의 3차원 형태 때문에 헷갈리는 부분이 있었는데, 차근차근 읽다보면 쉽게 이해가 가능 할 것으로 보인다.
마지막으로, 정책 반복 시 정책 평가의 역할과 정책 개선에 대한 이해가 필수적이라 생각하고, 상태가치함수, 행동가치함수, 정책함수간의 관계에 대한 지식이 반드시 동반되어야 한다고 생각한다.
참고자료 :
아인슈타인 합 계산방식 : ita9naiwa.github.io/numeric%20calculation/2018/11/10/Einsum.html
완비 거리공간 : freshrimpsushi.tistory.com/1425
강화학습 A-Z 강의자료
'강화학습 강의 복습노트' 카테고리의 다른 글
| Part2 - 5. 몬테 카를로 정책추정 (Monte-carlo prediction: MC prediction) (0) | 2020.12.25 |
|---|---|
| Part2 - 4. 비동기적 동적계획법 (0) | 2020.12.23 |
| Part2 - 2. MDP(Markov Decision Processes) (0) | 2020.12.21 |
| Part2 - 1. MP, MRP (0) | 2020.12.21 |
| Part1 - 1. 강화학습의 기본개념 (0) | 2020.12.21 |



