Part2 - 1. MP, MRP

1) 강화학습 문제와 가치기반 강화학습 문제의 풀이 기법

그림1. 환경에 대한 정보유무에 따른 강화학습 문제 풀이기법

---

2) 이번 chapter에서 익혀야 할 개념

2-1) MDP (Markov Decision Process) : 마르코프 결정과정

  -  "강화학습 문제"를 기술하는 수학적 표현방법

  -  마르코프 결정과정을 쉽게 이해하기 위해서는

     MC(Markov Chain), MRP(Markov Reward Process)에 대한 이해가 필요

 

2-2) MC (Markov Chain) : 마르코프 과정 또는 마르코프 체인

  -  마르코프 특성(Markov Property)을 따르는 과정을 뜻함

* 마르코프 특성과 체인에 대한 기본 개념은 알고 있을 것으로 생각하고 진행한다.

  -  MC <$S,P$> 인 튜플

     $S$ : 유한한 상태의 집합

     $P$ : 상태 천이 행렬 (State Transition Matrix)

그림2. 상태 천이 행렬

 

2-3) MRP (Markov Reward Process) : 마르코프 보상과정

  -  MC에 보상을 추가한 확률 과정

  -  MRP <$S,P$,$R,\gamma$> 인 튜플

     $R$ : 보상함수. ($R$ : $S\rightarrow \mathbb{R}$)

     $\gamma$ : 감소율. ($\gamma \in [0,1]$)

* 감소율은 왜 필요한가?  ->  뒤에서 확인해보겠다.

 

2-4) 리턴 (Return) : 시점 $t$부터 전체 미래에 대한 "감가된 보상의 합"

 

그림3. 리턴 계산 수식

  -  리턴은 강화학습 agent가 현재 상태로부터 미래의 일을 고려할 수 있게 해주는 장치이다.

  -  $\gamma$ = 0 : 미래에 대한 고려 X (바로 다음의 보상만 추구하게 될 것)

  -  $\gamma$ -> 1 : 미래에 대한 고려가 커짐

  -  $R_t$는 미래의 어떤 시점에서 획득하는 보상 : 확률변수임

 

---

그렇다면 여기서, 리턴은 왜 감가하는 것인가? (감소율은 왜 필요한가?) 

  1. 감가하면 값이 무한히 커지는 것을 방지, 계산이 수월해진다.

  2. 수학적인 분석이 쉬워진다.

  3. '먼 미래는 불확실하다'는 철학을 반영

  4. 사람은 먼 미래에 실현되는 이익을 선호하지 않는다.

---

 

2-5) 가치 함수 (Value function) : 현재상태 s에서 리턴($G_t$)의 기댓값

$$ V(s) : \mathbb {E}[G_t|S_t = s]$$

  -  말 그대로 현재시점 $t$에서 상태가 s이면 미래의 기대 리턴은 얼마인지 구하는 것이다.

  -  $G_t$는 위의 수식을 참고하자.

 

3) Bellman 기대 방정식 (Bellman Expectation Equation : BEE)

그림4. Bellman Expectation Equation의 풀이

* (4) -> (5) 에서는 $\mathbb{E}[A] = \mathbb{E}[\mathbb{E}[A]]$을 활용

 

$V(s)$와 $G_t$의 구조를 잘 기억하고 있어야 한다! 나중에 MC, TD모델을 보다보면 헷갈릴 때가 있다.

 

---

그림5. Bellman Expectation Equation의 풀이

  -  그림4에서 얻은 식을 재귀적 형태로 만들면 그림5의 식을 얻을 수 있다.  (단 $s'$는 다음상태)

---

위의 식을 matrix표현으로 표현하면 다음과 같다.

그림6. BEE의 선형식 형태

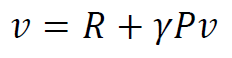
  -  $v$ : 모든 상태의 value function값을 담은 벡터

  -  $R$ : 모든 상태의 reward function값을 담은 벡터

  -  $\gamma$ : 감가율

  -  $P$ : 상태 천이 매트릭스

그림7. BEE의 선형식 형태

  -  여기서 $n$은 모든 상태의 수이다.

  -  이 식은 그림8과 같이 직접해를 구할 수 있다.

그림8. BEE의 풀이법

하지만 큰 문제가 있다. 상태의 수 $n$이 커질 수록 문제를 푸는것이 어려워진다! (시간도 엄청나게 걸림)

 

 BUT, 뒤에서 나올 DP, MC, TD기법을 사용하면 직접해를 구하지 않더라도 문제를 쉽게 풀 수 있다.

---

내 생각:

기존에 Markov Chain에 대한 개념만 알고 있던터라 처음 MRP, MDP을 들었을 때 개념이 모호했다.

 

그리고 여기서 Bellman Expectation Equation의 한계점이 아주 눈에 띈다.

실생활에서 적용 시켜야 할 강화학습의 경우 n이 작은 경우는 거의 눈을 씻고 찾아도 잘 없을 것이다.

 

그래서 BEE는 상태의 수가 적은 공간에서 직접해를 구해, 타 알고리즘의 에러값을 비교하는 정도로 쓰일 수 밖에 없을 것 같다.

 

참고자료 :

강화학습 A-Z 강의노트

대소니님의 블로그 : 강화학습 기초

RL (강화학습) 기초 - 3. Markov Decision Processes (1)