Part2 - 10. Off-policy TD control

지난 포스트에서 봤던 TD($\lambda$)와 Off-policy MC에 대해 정리해보자.

 

(1) TD학습 알고리즘의 형태

 

$$ V(s) \leftarrow V(s) + \alpha(G_t - V(s))$$

 

TD(0)의 경우

$G_t$ $\overset{def}{=} R_{t+1} + \gamma V(S_{t+1})$

 

TD target  :  $G_t$

TD error  :  $\delta_t = G_t - V(S_t) = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)$ 

 

(2) Off-policy MC알고리즘

 

  -  임의의 행동 정책함수 $\mu$ 로 에피소드 생성

 

  -  $G_t^{\pi/\mu}$ = $\prod _{k = t}^{T-1} \frac{\pi(A_k|S_k)}{\mu(A_k|S_k)} G_t$

 

  -  MC 업데이트

$$ Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha (G_t^{\pi/\mu} - Q(s_t,a_t))$$

 

On-policy와 Off-policy의 가장 큰 차이점!!

On-policy : 행동정책 $\mu$와 평가정책$\pi$가 동일!

Off-policy : 행동정책 $\mu$와 평가정책 $\pi$가 다름!

 

 

그렇다면 이번에는 Off-policy TD에 대해 알아보자

1) Importance sampling for Off-policy TD

  -  임의의 행동 정책함수 $\mu$ 로 에피소드 생성

  -  TD target : $R_{t+1} + \gamma V(S_{t+1})$ 계산

  -  Importance sampling corrected TD 업데이트 수행

 

$V(s_t) \leftarrow V(s_t) + \alpha$ ( $\frac{\pi(a_t|s_t)}{\mu(a_t|s_t)}$ ( $R_{t+1} + \gamma V(s_{t+1})$) $ - V(s_t)$ )

 

2) Importance sampling - Off policy control의 단점

이렇게 Importance sampling을 활용한 Off-policy control들에는 단점이 있다.

(1) Sampling distribution (행동정책 $\mu(a_t|s_t)$)의 선택에 따라 추산치의 분산이 커질 수 있다.

     ex. 현재 평가 정책 $\pi$와 상이하게 다른 $\mu$를 사용하면 분산이 매우 커짐

     따라서 아무 분포로 exploration해도 되지만 분산 문제가 생길 가능성이 있다.

 

(2) 구현이 귀찮다. 추가적으로 $\mu(a_t|s_t)$도 기록해야한다.

 

그렇다면 Importance sampling이 없는 off-policy 학습방법은 없을까?

 

3) Q - Learning : An Off-policy TD Control

Q-Learning은 Importance Sampling이 없는 TD control이다.

 

Q-Learning 알고리즘의 의사코드를 살펴보자

그림1. Q-Learning 알고리즘의 Pseudo Code

앞에서 본 SARSA알고리즘과 비슷해보인다.

 

그림2. SARSA알고리즘의 Pseudo Code

 

차이점을 살펴보면

(1) Q-Learning의 경우 next action이 필요하지 않다는 것

(2) SARSA는 On-policy, Q-Learning은 Off-policy라는 점이 있다.

 

SARSA 알고리즘은 current action $a$와 next action $a'$까지 동일한 정책을 사용하여 결정하는 반면

Q-Learning 알고리즘은 행동 a를 결정 할 때는 행동정책 $\mu$를,

$Q(s,a)$를 업데이트 하기 전 next action $a'$을 정할 때에는 평가정책 $\pi$를 사용한다.

 

여기서 Q-Learning의 평가정책 $\pi$는 Greedy Policy를 따르며 형태는 다음과 같다.

그림3. Q-Learning의 평가정책

 

Q-Learning 알고리즘은 앞서 포스팅한 SARSA기법에서 update_sample만 수정되었다.

update_sample함수의 Python 코드를 구현하면 다음과 같다.

 

def update_sample(self, state, action, reward, next_state, done):
    s, a, r, ns = state, action, reward, next_state
    # Q-Learning target
    td_target = r + self.gamma * self.q[ns, :].max() * (1 - done)
    self.q[s, a] += self.lr * (td_target - self.q[s, a])

함수의 인자로 더이상 next_action을 받아오지 않으며

td_target을 구할 때 self.q[ns, :].max()를 통해 optimal한 행동에 대한 Q값을 구하는 것을 볼 수 있다.

 

전체적인 코드를 참고하고자 하면 이전포스트를 참고하기 바란다.

Part2 - 8. SARSA : TD기법을 활용한 최적 정책 찾기

 

 

Q-Learning 알고리즘을 보면 Importance Sampling이 사라졌다.

어떻게 가능한 것일까?

 

이를 확인하기 위해 Bellman 최적 방정식(BOE)과 가치반복 알고리즘에 대해 다시보자.

그림4. Bellman Optimality Equation

그림5. 가치반복 알고리즘의 Pseudo code

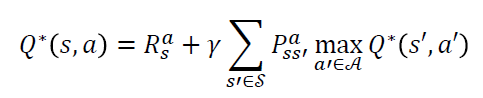
가치반복은 반복적으로 Bellman optimal backup을 진행함으로써 Bellman 최적 방정식의 해를 구하는 기법이었다.

 

샘플이 1개이며 Incremental update 한다고 가정하고 Bellman 최적 방정식의 샘플기반 추산을 살펴보면

그림6. Bellman 최적 방정식의 샘플기반 추산

Optimal한 행동가치함수 Q의 값은 $r + \gamma \underset{a'}{max} Q(s',a')$이 된다.

 

추산치가 행동정책 $\mu$ 및 평가정책 $\pi$의 영향을 받지 않아 Importance sampling을 할 이유가 사라지는 것이다.

 

4) Q - Learning의 단점

Q - Learning은 Importance sampling 없이 off-policy learning이 가능하다는 장점이 있다.

 

하지만 Maximization bias라는 단점이 존재한다.

 

Maximizaiont bias : Q-Learner가 가치함수 Q(s,a)를 실제값보다 높게 평가하는 문제

 

5) SARSA vs. Q-Learning 성능비교

SARSA와 Q-Learning의 성능비교를 위해 사용할 환경은 CliffWalking이라는 환경이다.

 

그림7. Cliff Walking환경의 형태

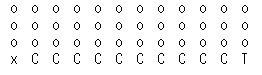
1. 행동공간은 상,하,좌,우 총 4개의 행동이 존재.

2. 초기상태 $s_0$는 X로 표시되어있으며 종결상태는 T로 표시된 곳이다.

3. 매 이동마다 보상 -1을 받는다.

4. C는 절벽이며 절벽에 도달하면 보상 -100을받고 초기상태 X로 돌아간다.

 

2개의 agent를 각각 SARSA, Q-Learning으로 학습시킨 후 episode별 Reward를 비교하면 다음과 같다.

그림8. SARSA vs. Q-Learning

 

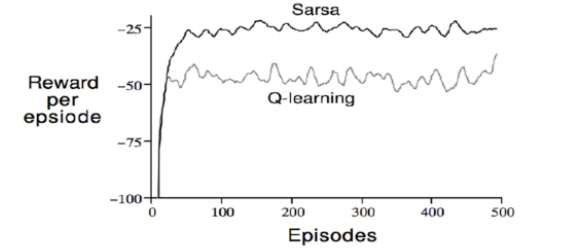
Off-policy인 Q-Learning의 보상이 On-policy인 SARSA의 보상보다 더 낮다. 왜일까?

 

그림9. SARSA vs. Q-Learning

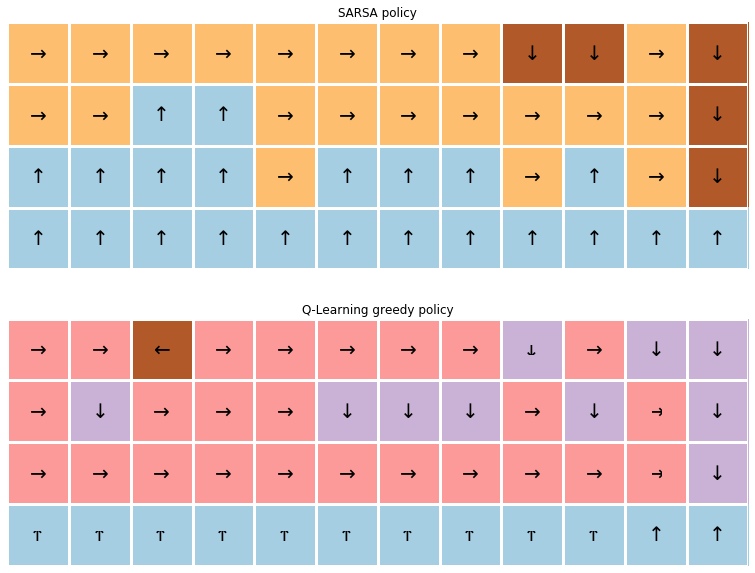
그림9.에서 보이는 화살표는 각 상태에서 어느 방향으로 가는 것이 (어떤 action을 취하는 것이 가장 좋은지 = 어떤 행동에 대한 Q값이 가장 큰지)를 보여준다.

 

SARSA를 선택하는 policy의 경우 좀더 safe한 선택을 한다. optimal한 policy를 찾기가 어렵다.

Reward만으로는 optimal한 policy를 찾기 어렵고, 주로 실험을 하며 실제로 run을 하는 동안 우리가 원하는 대로 agent가 행동을 하는지 체크해야한다.

 

내 생각 :

Q-Learning의 Maximization bias 문제를 해결 하기 위해서는 어떻게 해야할까

DQN에 대해서도 많이 들었는데 추후에 배울 DQN기법은 Maximization bias문제를 해결 할 수 있을까?

 

아직 개념에 대한 이해가 많이 부족한 것같다. 아니면 내 기억력이 부족한건지..

한 Part를 끝내고 나서 그때 강의에 대해 들었던 기억력으로 복습노트를 작성하다보니 헷갈리는게 많다.

시간을 내서 다시한번 쭉 돌아보는 시간을 가져야겠다.

참고자료 :

[1] 강화학습 A-Z 강의자료

[2] cding.tistory.com/53

[3] sumniya.tistory.com/15?category=781573